Read In Pursuit of the Unknown Online
Authors: Ian Stewart
In Pursuit of the Unknown (5 page)
Fig 9
Curvature of a surface.
Left
: zero curvature.
Middle:
positive curvature.
right
: negative curvature.
The plane of Euclid is flat, curvature zero. A sphere has the same curvature everywhere, and it is positive: near any point it looks like a
dome. (As a technical fine point: great circles meet in two points, not one as Euclid's axioms require, so spherical geometry is modified by identifying antipodal points on the sphere â considering them to be identical. The surface becomes a so-called projective plane and the geometry is called elliptic.) A surface of constant negative curvature also exists: near any point, it looks like a saddle. This surface is called the hyperbolic plane, and it can be represented in several entirely prosaic ways. Perhaps the simplest is to consider it as the interior of a circular disc, and to define âline' as an arc of a circle meeting the edge of the disc at right angles (
Figure 10
).

Fig 10
Disc model of the hyperbolic plane. All three lines through
P
fail to meet line
L
.
It might seem that, while plane geometry might be non-Euclidean, this must be impossible for the geometry of space. You can bend a surface by pushing it into a third dimension, but you can't bend
space
because there's no room for an extra dimension along which to push it. However, this is a rather naive view. For example, we can model three-dimensional hyperbolic space using the interior of a sphere. Lines are modelled as arcs of circles that meet the boundary at right angles, and planes are modelled as parts of spheres that meet the boundary at right angles. This geometry is three-dimensional, satisfies all of Euclid's axioms except the Fifth, and in a sense that can be pinned down it defines a curved three-dimensional space. But it's not curved round anything, or in any new direction.
It's just curved.
With all these new geometries available, a new point of view began to occupy centre stage â but as physics, not mathematics. Since space doesn't
have
to be Euclidean, what shape
is
it? Scientists realised that they didn't actually know. In 1813, Gauss, knowing that in a curved space the angles of a triangle do not add to 180°, measured the angles of a triangle formed by three mountains â the Brocken, the Hohehagen, and the Inselberg. He obtained a sum 15 seconds of arc greater than 180°. If correct, this indicated that space (in that region, at least) was positively curved. But
you'd need a far larger triangle, and far more accurate measurements, to eliminate observational errors. So Gauss's observations were inconclusive. Space might be Euclidean, and then again, it might not be.
My remark that three-dimensional hyperbolic space is âjust curved' depends on a new point of view about curvature, which also goes back to Gauss. The sphere has constant positive curvature, and the hyperbolic plane has constant negative curvature. But the curvature of a surface doesn't have to be constant. It might be sharply curved in some places, less sharply curved in others. Indeed, it might be positive in some regions but negative in others. The curvature could vary continuously from place to place. If the surface looks like a dog's bone, then the blobs at the ends are positively curved but the part that joins them is negatively curved.
Gauss searched for a formula to characterise the curvature of a surface at any point. When he eventually found it, and published it in his
Disquisitiones Generales Circa Superficies Curva
(âGeneral Research on Curved Surfaces') of 1828, he named it the âremarkable theorem'. What was so remarkable? Gauss had started from the naive view of curvature: embed the surface in three-dimensional space and calculate how bent it is. But the answer told him that this surrounding space didn't matter. It didn't enter into the formula. He wrote: âThe formula . . . leads itself to the remarkable theorem: If a curved surface is developed upon any other surface whatever, the measure of curvature in each point remains unchanged.' By âdeveloped' he meant âwrapped round'.
Take a flat sheet of paper, zero curvature. Now wrap it round a bottle. If the bottle is cylindrical the paper fits perfectly, without being folded, stretched, or torn. It is bent as far as visual appearance goes, but it's a trivial kind of bending, because it hasn't changed geometry on the paper in any way. It's just changed how the paper relates to the surrounding space. Draw a right-angled triangle on the flat paper, measure its sides, check Pythagoras. Now wrap the diagram round a bottle. The lengths of sides,
measured along the paper
, don't change. Pythagoras is still true.
The surface of a sphere, however, has nonzero curvature. So it is not possible to wrap a sheet of paper so that it fits snugly against a sphere, without folding it, stretching it, or tearing it. Geometry on a sphere is intrinsically different from geometry on a plane. For example, the Earth's equator and the lines of longitude for 0° and 90° to its north determine a triangle that has three right angles and three equal sides (assuming the Earth to be a sphere). So Pythagoras's equation is false.
Today we call curvature in its intrinsic sense âGaussian curvature'. Gauss explained why it is important using a vivid analogy, still current. Imagine an ant confined to the surface. How can it work out whether the surface is curved? It can't step outside the surface to see whether it looks bent. But it can use Gauss's formula by making suitable measurements purely within the surface. We are in the same position as the ant when we try to figure out the true geometry of our space. We can't step outside it. Before we can emulate the ant by taking measurements, however, we need a formula for the curvature of a space of three dimensions. Gauss didn't have one. But one of his students, in a fit of recklessness, claimed that he did.
The student was Georg Bernhard Riemann, and he was trying to achieve what German universities call Habilitation, the next step after a PhD. In Riemann's day this meant that you could charge students a fee for your lectures. Then and now, gaining Habilitation requires presenting your research in a public lecture that is also an examination. The candidate offers several topics, and the examiner, which in Riemann's case was Gauss, chooses one. Riemann, a brilliant mathematical talent, listed several orthodox topics that he knew backwards, but in a rush of blood to the brain he also suggested âOn the hypotheses which lie at the foundation of geometry'. Gauss had long been interested in just that, and he naturally selected it for Riemann's examination.
Riemann instantly regretted offering something so challenging. He had a hearty dislike of public speaking, and he hadn't thought the mathematics through in detail. He just had some vague, though fascinating, ideas about curved space. In
any
number of dimensions. What Gauss had done for two dimensions, with his remarkable theorem, Riemann wanted to do in as many dimensions as you like. Now he had to perform, and fast. The lecture was looming. The pressure nearly gave him a nervous breakdown, and his day job helping Gauss's collaborator Wilhelm Weber with experiments in electricity didn't help. Well, maybe it did, because while Riemann was thinking about the relation between electrical and magnetic forces in the day job, he realised that force can be related to curvature. Working backwards, he could use the mathematics of forces to define curvature, as required for his examination.
In 1854 Riemann delivered his lecture, which was warmly received, and no wonder. He began by defining what he called a âmanifold', in the sense of many-foldedness. Formally, a âmanifold', is specified by a system
of many coordinates, together with a formula for the distance between nearby points, now called a Riemannian metric. Informally, a manifold is a multidimensional space in all its glory. The climax of Riemann's lecture was a formula that generalised Gauss's remarkable theorem: it defined the curvature of the manifold solely in terms of its metric. And it is here that the tale comes full circle like the snake Orobouros and swallows its own tail, because the metric contains visible remnants of Pythagoras.
Suppose, for example, that the manifold has three dimensions. Let the coordinates of a point be (
x
,
y
,
z
), and let (
x
+ d
x
,
y
+ d
y
,
z
+ d
z
) be a nearby point, where the d means âa little bit of'. If the space is Euclidean, with zero curvature, the distance d
s
between these two points satisfies the equation
d
s
2
= d
x
2
+ d
y
2
+ d
z
2
and this is just Pythagoras, restricted to points that are close together. If the space is curved, with variable curvature from point to point, the analogous formula, the metric, looks like this:
d
s
2
=
X
d
x
2
+ Y d
y
2
+ Z d
z
2
+ 2
U
d
x
d
y
+ 2
V
d
x
d
z
+ 2
W
d
y
d
z
Here
X, Y, Z, U, V, W
can depend on
x, y
and z. It may seem a bit of a mouthful, but like Pythagoras's equation it involves sums of squares (and closely related products of two quantities like
dx dy
) plus a few bells and whistles. The 2s occur because the formula can be packaged as a 3 Ã 3 table, or matrix:
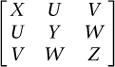
where
X, Y, Z
appear once, but
U, V, W
appear twice. The table is symmetric about its diagonal; in the language of differential geometry it is a symmetric tensor. Riemann's generalisation of Gauss's remarkable theorem is a formula for the curvature of the manifold, at any given point, in terms of this tensor. In the special case when Pythagoras applies, the curvature turns out to be zero. So the validity of Pythagoras's equation is a test for the absence of curvature.
Like Gauss's formula, Riemann's expression for curvature depends only on the manifold's metric. An ant confined to the manifold could observe the metric by measuring tiny triangles and computing the curvature. Curvature is an intrinsic property of a manifold, independent of any surrounding space. Indeed, the metric already determines the geometry, so no surrounding space is required. In particular, we human ants can ask
what shape our vast and mysterious universe is, and hope to answer it by making observations that do not require us to step outside the universe. Which is just as well, because we can't.
Riemann found his formula by using forces to define geometry. Fifty years later, Einstein turned Riemann's idea on its head, using geometry to define the force of gravity in his general theory of relativity, and inspiring new ideas about the shape of the universe: see
Chapter 13
. It's an astonishing progression of events. Pythagoras's equation first came into being around 3500 years ago to measure a farmer's land. Its extension to triangles without right angles, and triangles on a sphere, allowed us to map our continents and measure our planet. And a remarkable generalisation lets us measure the shape of the universe. Big ideas have small beginnings.
| 2 | Shortening the proceedings |